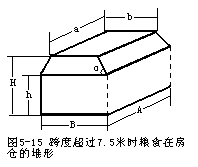
一、房仓散装容量的计算

　　房仓散装（见图5-15）容量的计算，可以按照下列简单公式进行计算：

　　Em≈r[ABh + ((A+a)/2)*((B+b)/2)*(H-h)]

　　式中：Em---房仓仓容量；r---粮食的容量；A---房仓的内部长度（米）；a---谷物装载后，水平表面的长度（米）；B---房仓的内部宽度（米）；b---谷物装载后水平面的宽度（米）；H---谷物装载后，中央部分的高度（米）；h---谷物装载后，沿壁部分的高度（米）。

　　粮食装载后，其上部水平表面的数值a和b，可以

用下列算式算出：

　　a=A-2(H-h)ctgα

　　式中：α---谷物装载的倾斜角。

　　如果α角为25度，则：a=A-4.29(H-h) b=B-4.29(H-h)

　　a和b的近似值通常采用：a=A-5(H-h) b=B-5(H-h)

　　二、筒仓仓容量的计算

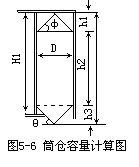
　　圆型立筒仓（见图5-16）的容量可以用下式求得：

　　E'm=r(πD2/4)[H'-D/3(tgφ+tgθ)]

　　式中：r---粮食的容重；H'---筒仓顶板至卸粮漏斗口的距离（米）；D---圆形筒仓的内径（米）；φ---粮食的静止角；θ---筒仓卸粮漏斗倾角。

　　根据计算证明，对于高为30米，直径为6米的标准圆形筒仓，或近似于标准的筒仓，在计算式的后半段的数值是很小的，因此可以近似地用下式表示：

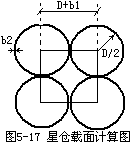
　　对于圆形筒仓之间星仓（见图5-17）的仓容量可按下式计算：

　　e'm1=0.9[(D+b1)2-(π(D+2b2)2)/4]rH

　　em1=0.9e'm1

　　式中：b1---为两相邻筒仓之间的壁厚；b2---为仓筒壁厚。

　　行列式排列的圆形筒仓筒体行列的数目是已知的，以（m*n)代表大筒仓数目，以(m-1)(n-1)代表星仓的数目，因此筒仓每个筒体的仓容量应该为：

　　Em=mnem+(m-1)(n-1)em1

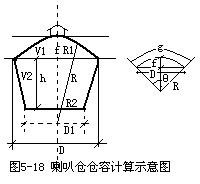
　　三、喇叭仓仓容计算

　　喇叭仓（见图5-18）的仓容可用下面的公式求得：

　　Em=[πh/3(R21+R1R2+R22)+0.95πf2/3(3R-f)]r

　　式中：Em---仓容量；R1、R2---喇叭筒上、下口半径；h---喇叭仓筒高；f---壳顶矢高（f≈D/5)；R---壳顶的曲率半径，R=（4f2+D)/8f。

　　喇叭仓的装粮方式需要时可装至入粮口，可用上述公式计算，